Cамоучитель по Visual Studio.Net
Трехточечный шаблон аппроксимации второй производной
Рисунок 11.2. Трехточечный шаблон аппроксимации второй производной
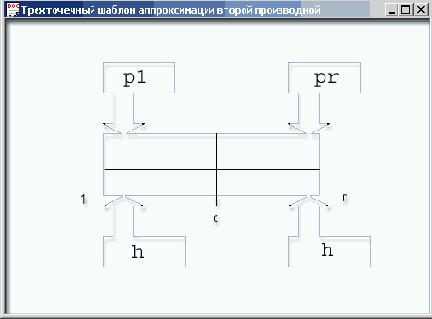
Мы имеем три точки и два отрезка, которых вполне достаточно, чтобы справиться со второй производной при попытке ее приближенного вычисления. Индексы 1, г и с означают left, right и center. Обозначение pi принято для коэффициента, учитывающего свойства среды левого отрезка, например теплопроводности, а рг — правого. Шаги разбиения области вдоль оси х считаются одинаковыми и равными h. Теперь вы должны представить себе, что центр этого шаблона по очереди приставляется ко всем точкам из множества М. В результате этой процедуры мы по одному будем получать все |М| = N - 1 алгебраических уравнений, приближенно заменяющих одно дифференциальное уравнение Пуассона, которое, как говорят физики, удовлетворяется во всех точках этой части реального пространства.
Возвращаясь к шаблону из трех точек, напомним, что производная по х — это в некотором роде степень изменения функции, то есть скорость ее роста или падения вдоль этой координаты. Приближенно она равна:
dU/dx=(Ur-Uc)/h
для правого отрезка и
dU/dx=(Uc-Ul)/h
для левого. Теперь надо записать приближенную оценку для второй производной с учетом коэффициента теплопроводности. Он может иметь разные значения (р! и рг) в левой и в правой частях шаблона:
d/dx(pdU/dx)={(pr[Ur-Uc])/h-(pl[Uc-Ul])/h}/h (2)
Произведя подстановку в исходное дифференциальное уравнение (1) и упростив выражение, получим алгебраическое уравнение:
aUl+bUc+cUr=0 (3)
связывающее температуры трех соседних узлов сетки с физическими свойствами прилежащих участков пространства, так как значения коэффициентов уравнения зависят от р, k и h:
a=pl/h^2; c=pr/h^2; b=-a-c+k; (4)
Коэффициент а описывает свойства левой части шаблона, а с — правой, а Ь — обеих вместе. Чуть позже мы увидим, что коэффициент b попадет в диагональ матрицы. Теперь надо примерить шаблон ко всем узлам сетки. Узел номер 1 даст уравнение:
a1U0+b1U1+c1U2=0,
узел номер 2:
a2U1+b2U2+c2U3=0,
и т. д. Здесь важно следить за индексами. Для простоты пока считаем, что коэффициенты а,, b,, с, не изменяются при переходе от узла к узлу. В узлах сетки вблизи границ (то есть в узле 1 и узле N-1) уравнения упрощаются, так как £/„ и UN считаются известными и поэтому перемещаются в правую часть уравнения. Так, первое уравнение системы станет:
b1U1+c1U2=0,
а последнее:
an-1Un-2+bn-1Un=+1=0,
Все остальные уравнения будут иметь вид (3). Теперь пора изобразить всю систему уравнений, используя матричные обозначения и не отображая многочисленные нули. Для простоты будем считать, что N = 5:
| b1 | c1 | U1 | -a1U0 | |||
| a2 | b2 | c2 | U2 | 0 | ||
| a3 | b3 | c3 | U3 | = | 0 | |
| a4 | b4 | U4 | -c4U5 |
Вы видите, что матрица системы уравнений имеет характерную регулярную трех-диагональную структуру, а структура вектора правых частей тоже легко прочитывается. Граничные; условия краевой задачи заняли подобающие им крайние места, а внутренние позиции — нули.
Решать такую систему следует специальным методом, который называется методом прогонки и является модификацией метода Гаусса. Он работает во много раз быстрее самого метода Гаусса. Мы реализуем его немного позже, а сейчас попробуем применить алгоритм generate из библиотеки STL для генерации матрицы, имеющей рассмотренную структуру, и вектора решений U. В простых случаях он известен и легко угадывается. Затем с помощью сечений произведем умножение Матрицы на вектор и убедимся в том, что вектор правых частей системы уравнений будет иметь правильную структуру и значения. Эту часть работы рассматривайте как дополнительное упражнение по использованию структур данных типа valarray и slice. В процессе решения краевой задачи мы будем пользоваться контейнерами другого типа (vector), так как метод прогонки не требует применения каких-то особых приемов работы с сечениями.
Если для простоты принять р = 1, h = 1, U0 = 100, a UN =0, то коэффициенты матрицы будут равны ai = сi = 1, bi. = -2 , k = 0, а решение U(x) известно заранее. Это — линейно спадающая от 100 до 0 функция, а в более общем случае — функция произвольных граничных условий:
U(x)=U0+[Un-U0]x/L
где L — длина всей расчетной области. Правильность решения проверяется прямой подстановкой в уравнение (1).